|
Streamer fluid modeling - An overview of ARCoS
1.0
|
|
Streamer fluid modeling - An overview of ARCoS
1.0
|
In a fluid model of a streamer, we replace the individual particles in the system by a density function  . The temporal evolution of this density function is governed by the physical processes of the system and this model takes the form of a set of partial differential equations (PDEs). The derivation of this so-called classical streamer model starts from the continuity equation. For particle species
. The temporal evolution of this density function is governed by the physical processes of the system and this model takes the form of a set of partial differential equations (PDEs). The derivation of this so-called classical streamer model starts from the continuity equation. For particle species 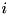 , we have:
, we have:
![\[ \frac{\partial n_i(\mathbf{r},t)}{\partial t} + \nabla \cdot \mathbf{j}_i(\mathbf{r},t) = S_i(\mathbf{r},t). \]](form_27.png)
Here 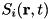 represents the total of all sources and sinks of species
represents the total of all sources and sinks of species 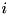 .
. 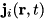 is the term for the particle current density of species
is the term for the particle current density of species 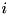 . Particles can drift and diffuse as described by the following expression for the particle current density
. Particles can drift and diffuse as described by the following expression for the particle current density 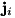 :
:
![\[ \mathbf{j}_i(\mathbf{r},t) = \mu_i n_i(\mathbf{r},t) \mathbf{E}(\mathbf{r},t) - D_i \nabla n_i (\mathbf{r},t). \]](form_31.png)
In the above equation, the first term represents the particle drift due to the electric field, with 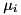 the mobility coefficient of species
the mobility coefficient of species 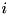 . The second term represents the diffusion of particles due to the spatial gradient in particle densities with diffusion coefficient
. The second term represents the diffusion of particles due to the spatial gradient in particle densities with diffusion coefficient 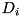 . These equations can be derived from the Boltzmann equation
. These equations can be derived from the Boltzmann equation
On the timescales involved, we consider only electrons to be mobile, while ions and neutrals remain stationary, which means that for heavy species, the continuity equation is reduced to
![\[ \frac{\partial n_i(\mathbf{r},t)}{\partial t} = S_i(\mathbf{r},t). \]](form_34.png)
The sources and sinks in the first equation play a very important role in the dynamics of the streamer. In this model, the sources and sinks correspond to reactions between the different charged and neutral species present in the gas. The source term due to a single reaction is the product of the densities of the species involved in the reaction and the field-dependent rate coefficient for that reaction.
As an example, the impact ionization reaction
![\[ e^- + \mathbf{N}_2 \rightarrow 2 e^- + \mathbf{N}_2^+ \]](form_35.png)
is modeled by
![\[ S_{ionization} = k_{ion}(|\mathbf{E}|) n_e [\mathbf{N}_2]. \]](form_36.png)
Here 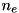 is the local electron density,
is the local electron density, ![$[\mbox{N}_2]$](form_38.png) the density of
the density of  and
and 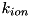 the reaction coefficient for impact ionization depending on the magnitude of the local electric field. The value of
the reaction coefficient for impact ionization depending on the magnitude of the local electric field. The value of 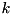 can be determined in different ways, from experiments, theoretical calculations or simulations. The traditional approximation suggested by Townsend uses an empirical expression for the impact ionization term, see the book by Y. P. Raizer, "Gas Discharge Physics":
can be determined in different ways, from experiments, theoretical calculations or simulations. The traditional approximation suggested by Townsend uses an empirical expression for the impact ionization term, see the book by Y. P. Raizer, "Gas Discharge Physics":
![\[ \frac{dn_e}{dt} = n_e \mu_e |\mathbf{E}| \alpha_0 e^{-E_0 / |\mathbf{E}|}, \]](form_42.png)
where 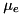 is the electron mobility coefficient,
is the electron mobility coefficient, 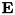 is the local electric field and
is the local electric field and 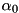 and
and 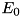 are parameters that can be determined by fitting experimental data. In gases that contain an electronegative admixture, such as
are parameters that can be determined by fitting experimental data. In gases that contain an electronegative admixture, such as 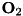 , the process of attachment can provide a sink for the electron density through the following reactions:
, the process of attachment can provide a sink for the electron density through the following reactions:
![\[ e^- + \mathbf{O}_2 \rightarrow \mathbf{O} + \mathbf{O}^- \]](form_48.png)
![\[ e^- + \mathbf{O}_2 + \mathbf{O}_2 \rightarrow \mathbf{O}_2^- + \mathbf{O}_2 \]](form_49.png)
The first attachment process is dissociative attachment, the second an example of a 3-body attachment (a 3-body attachment can also occur with an oxygen and nitrogen molecule). In the case of the 3-body attachment, the reaction rate scales with the square of the oxygen density:
![\[ S_{3-body-att} = k_{3-body-att}(|\mathbf{E}|) n_e [\mathbf{O}_2]^2. \]](form_50.png)
Further ionization losses can occur via one or more recombination processes, but these typically have a timescale that is much longer than the timescale of streamer development and propagation and are therefore primarily interesting for the evolution of the charge density after a streamer discharge, as discussed in PhD Thesis Wormeester(to appear in 2013), Chapter 5.
In gases with attachment, detachment may occur, resulting in an additional source of electrons. In gases that contain both nitrogen and oxygen, the photoionization process provides a non-local source of electrons. Since photoionization is non-local, it can not be modelled by simple reaction equations such as the ones for impact ionization. Instead, the local contribution of photoionization is calculated by spatially integrating contributions from the entire domain. The commonly used model for photoionization and the approximations made to make this model suitable for simulation are discussed in PhD Thesis Wormeester(to appear in 2013), Chapter 3, section Photoionization.
The reaction model for streamer simulations can be very minimal or very extended, with many species and reactions, including metastables and various excited states. The complexity of the reaction model depends on the purpose of the simulations. For negative streamers in nitrogen, a model containing no more than three species (  ,
,  and
and 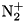 ) and one reaction (impact ionization) is sufficient to simulate the dynamics of the streamer head, see Montijn et al. For more detailed studies of the streamer chemistry, the reaction model should be as complete as possible.
) and one reaction (impact ionization) is sufficient to simulate the dynamics of the streamer head, see Montijn et al. For more detailed studies of the streamer chemistry, the reaction model should be as complete as possible.
The streamer evolves under the influence of an electric field, which consists of an externally applied electric field and the electric field generated by space charges. These space charges are present at the head of the streamer as well as on the edge of the streamer channel. For the further propagation of the streamer, the enhanced electric field in front of the streamer, generated by the space charge in the streamer head is essential. We compute the net charge density 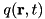 :
:
![\[ q(\mathbf{r},t) = e \sum_i q_i n_i(\mathbf{r},t), \]](form_54.png)
where for species 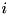 ,
, 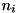 denotes the density function of these species and
denotes the density function of these species and 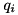 the charge of a particle in units of the electron charge
the charge of a particle in units of the electron charge 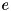 . From this we compute the potential by solving the Poisson equation
. From this we compute the potential by solving the Poisson equation
![\[ \nabla^2 \phi(\mathbf{r},t) = \frac{q(\mathbf{r},t)}{\epsilon_0} \]](form_58.png)
and the electric field
![\[ \mathbf{E}(\mathbf{r},t) = -\nabla \phi(\mathbf{r},t). \]](form_59.png)
The classical fluid model for streamers can be rescaled to dimensionless units and it is with these units that the code used in this documentation works. We refer the interested reader to the PhD thesis of Gideon Wormeester (to appear in 2013). From the Townsend approximation for ionization, a characteristic field and length scale emerges: 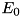 and
and 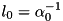 , respectively. The characteristic velocity follows from the drift velocity of electrons in the characteristic field,
, respectively. The characteristic velocity follows from the drift velocity of electrons in the characteristic field,
![\[ E_0: v_0 = \mu_e E_0. \]](form_61.png)
The characteristic number density follows from the Poisson equation. Values for 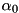 ,
, 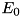 and
and 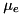 were obtained from PhD Thesis Montijn and are at standard temperature and pressure:
were obtained from PhD Thesis Montijn and are at standard temperature and pressure:
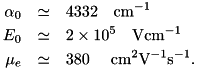
When we insert these values in the characteristic scales, we obtain the values with which to rescale the equations:
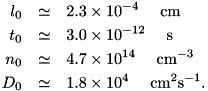
We can now make the appropriate substitutions ( 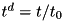 and similarly for the other variables; the superscript
and similarly for the other variables; the superscript 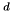 will be used to indicate that a variable is in dimensionless form, where this is not clear from the context. For clarity of reading, the superscript
will be used to indicate that a variable is in dimensionless form, where this is not clear from the context. For clarity of reading, the superscript 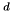 will be omitted where it is clear that variables are dimensionless) to obtain the classical fluid equations in dimensionless continuity form:
will be omitted where it is clear that variables are dimensionless) to obtain the classical fluid equations in dimensionless continuity form:
![\[ \partial_{t} + \nabla \cdot \mathbf{j}_i = S_i, \]](form_66.png)
where 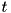 is the dimensionless time,
is the dimensionless time, 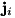 the dimensionless particle density current for species
the dimensionless particle density current for species 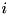 and
and 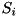 the dimensionless source term for species
the dimensionless source term for species 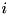 .
. 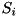 is obtained by rewriting reaction equations such as the impact ionization reaction equation in dimensionless form, where we remark that all rate-coefficients should also be rescaled. The particle density current
is obtained by rewriting reaction equations such as the impact ionization reaction equation in dimensionless form, where we remark that all rate-coefficients should also be rescaled. The particle density current 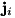 is obtained by rescaling expression into equation
is obtained by rescaling expression into equation
![\[ \mathbf{j}_i = -\mu_i n_i \mathbf{E} - D_i \nabla n_i, \]](form_69.png)
where 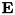 is the dimensionless electric field and
is the dimensionless electric field and 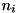 ,
, 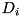 and
and 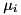 are the dimensionless particle density, diffusion coefficient and mobility respectively of species
are the dimensionless particle density, diffusion coefficient and mobility respectively of species 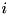 . We find that in dimensionless units
. We find that in dimensionless units 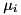 is equal to 1 while for heavy particles
is equal to 1 while for heavy particles 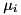 is taken as 0, since heavy particles are assumed to be stationary in this model. The dimensionless current density equation can therefore be simplified to
is taken as 0, since heavy particles are assumed to be stationary in this model. The dimensionless current density equation can therefore be simplified to
![\[ \mathbf{j}_e = -n_e \mathbf{E} - D_e \nabla n_e \]](form_70.png)
for electrons and 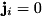 for heavy particles. The expression for the charge density equation
for heavy particles. The expression for the charge density equation 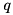 , is rescaled to
, is rescaled to
![\[ q(\mathbf{r},t) = \sum_i q_i n_i(\mathbf{r},t). \]](form_73.png)
The Poisson equation is rescaled to
![\[ \nabla^2 \phi = q. \]](form_74.png)
We remark that although the code described here internally works with the dimensionless equations and variables described in this section, all results are presented in regular units unless otherwise noted. Input parameters for the simulation code are expected to be in dimensionless units. Finally we note that the rescaling to dimensionless units does not change the structure of the equations, it is merely a rescaling to a different set of units, where the dimensionless units yield a set of equations where some constants (such as 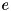 ,
, 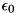 ,
, 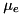 ) become unity.
) become unity.
We consider a cylindrical computational domain with coordinates:
![\[ (r,z,\theta) \in (0,L_r) \times (0,L_z) \times (0,2\pi). \]](form_76.png)
Although the code described here is capable of performing full 3D calculations, we assume cylindrical symmetry to greatly simplify the computations. For any spatially dependent function 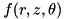 , we assume:
, we assume:  . Consequently, the coordinate system for our computations is limited to
. Consequently, the coordinate system for our computations is limited to 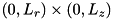 . We consider a setup with a powered electrode at
. We consider a setup with a powered electrode at 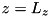 and a grounded electrode at
and a grounded electrode at 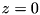 . If the powered electrode is a plate, the following boundary conditions are used for the electric potential
. If the powered electrode is a plate, the following boundary conditions are used for the electric potential  :
:
![\[ \begin{array}{llll} \forall z \; & \partial_r \phi(0,z,t) & = & 0\\ \forall r \; & \phi(L_r,z,t) & = & 0\\ \forall z \; & \phi(r,0,t) & = & 0\\ \forall r \; & \phi(r,L_z,t) & = & \phi_0 \end{array} \]](form_83.png)
with 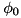 the potential applied to the powered electrode. If the powered electrode is a needle protruding from a plate, the needle has the same potential
the potential applied to the powered electrode. If the powered electrode is a needle protruding from a plate, the needle has the same potential 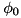 as the plate.
as the plate.

In Figure 1., the shaded rectangle represents the computational domain for the fluid equations, the thick horizontal lines the two planar electrodes with the needle and its parameters depicted at the anode. The area between the two planar electrodes is the computational domain for the Poisson equation. The needle is simulated by a single point charge, 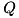 , chosen such that
, chosen such that 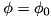 in the point
in the point 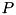 , which is the tip of the needle. The calculation assumes cylindrical symmetry around the needle axis represented by the dashed-dotted line.
, which is the tip of the needle. The calculation assumes cylindrical symmetry around the needle axis represented by the dashed-dotted line.
For the density equations, we use homogeneous Neumann conditions on all edges:
![\[ \partial_r n(0,z,t) = \partial_r n(L_r,z,t) = \partial_z n(r,0,t) = \partial_z n(r,L_z,t) = 0, \]](form_88.png)
where we remark that if the powered electrode is a needle, the computational domain for the density equations is smaller than the computational domain for the Poisson equation and the 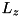 values for both domains are not equal. This difference is a requirement of the numerical implementation of the needle electrode and is further detailed in section Implementation of the needle-plane configuration.
values for both domains are not equal. This difference is a requirement of the numerical implementation of the needle electrode and is further detailed in section Implementation of the needle-plane configuration.
While the boundary conditions mentioned above are the ones used by Wormeester, the code that was used can also handle different choices of boundary conditions: both homogeneous Neumann and homogeneous Dirichlet boundary conditions are available for the top ( 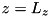 ), bottom (
), bottom ( 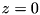 ) and right (
) and right ( 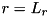 ) edges of the domain for both the densities and the potential. The Neumann condition on the central axis of the cylindrical domain is required for symmetry reasons.
) edges of the domain for both the densities and the potential. The Neumann condition on the central axis of the cylindrical domain is required for symmetry reasons.
As initial conditions for particle densities, two types of seeds are implemented in the code. A homogeneous seed, with a constant density over the entire domain and a Gaussian seed of the form
![\[ n(r,z,0) = n_{max} \mbox{exp}(-\frac{r^2 + (z - z_0)^2}{\sigma^2}). \]](form_91.png)
Here 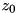 specifies the
specifies the 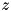 -coordinate of the maximum of the seed (which is located on the symmetry axis with
-coordinate of the maximum of the seed (which is located on the symmetry axis with 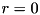 ), where the density is
), where the density is 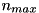 .
. 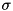 is a measure of the radius of the seed, it is the distance at which the density drops to
is a measure of the radius of the seed, it is the distance at which the density drops to 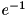 of the maximum value.
of the maximum value.
In typical streamer simulations, a seed of electrons and positive ions is placed at the tip of the needle to initiate the discharge. Other than these Gaussian seeds and the neutral background gas, initial particle densities are zero with the possible exception of added background ionization, a homogeneous density of negative and positive ions. The initial distribution of electrons and ions is charge neutral at every point of the domain.
The physical equations in section Fluid model are to be solved numerically. The computational code we have applied for this uses finite volume methods to solve a discretized version of the physical equations. Here we give a basic summary of the numerical technique used. For more details, the reader is referred to the work of Montijn et al., upon which the current code is based.
The dimensionless continuity and the dimensionless current density equations are discretized using finite volume methods and solved on a uniform rectangular grid with cells:
![\[ C_{ij} = [(i - 1) \Delta r, i \Delta r] \times [(j - 1) \Delta z, j \Delta z]\left(i = 1 , \cdots , \frac{L_r}{\Delta r}, j = 1 , \cdots , \frac{L_z}{\Delta z}\right), \]](form_97.png)
where  and
and 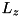 are the
are the 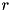 - and
- and 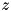 -dimensions of the grid and
-dimensions of the grid and 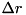 and
and 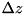 the size of a cell in
the size of a cell in 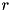 - and
- and 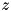 -direction, respectively. Particle density distributions are represented by their value in the cell center, which can be seen as an average over the cell. For some species
-direction, respectively. Particle density distributions are represented by their value in the cell center, which can be seen as an average over the cell. For some species  , we use
, we use 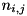 to denote the density at the cell center
to denote the density at the cell center 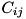 . For sake of clarity of notation we omit the superscript
. For sake of clarity of notation we omit the superscript 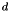 indicating that variables are in dimensionless units.
indicating that variables are in dimensionless units.
The discretized continuity equations in cylindrical coordinates, with cylindrical symmetry ( 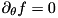 ) assumed, have the following form:
) assumed, have the following form:
![\[ \begin{array}{ll} \frac{d n_{i,j}}{d t} = & \frac{1}{r_i \Delta r} \Big(r_{i - \frac{1}{2}} F^a_{i - \frac{1}{2},j} - r_{i + \frac{1}{2}} F^a_{i + \frac{1}{2},j} + r_{i - \frac{1}{2}} F^d_{i - \frac{1}{2},j} - r_{i + \frac{1}{2}} F^d_{i + \frac{1}{2},j}\Big) + \\ & \frac{1}{\Delta z} \Big(F^a_{i,j - \frac{1}{2}} - F^a_{i,j + \frac{1}{2}} + F^d_{i,j - \frac{1}{2}} - F^d_{i,j + \frac{1}{2}}\Big) + S_{i,j}. \end{array} \]](form_106.png)
Here 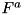 and
and  represent the advective and diffusive fluxes across the cell boundaries. Since we assume ions and neutral particles to be stationary, these terms are nonzero only for electrons. For heavy particles, only the source term
represent the advective and diffusive fluxes across the cell boundaries. Since we assume ions and neutral particles to be stationary, these terms are nonzero only for electrons. For heavy particles, only the source term 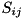 remains.
remains.
The advective flux, 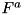 uses an upwind scheme with flux limiting and is defined as follows:
uses an upwind scheme with flux limiting and is defined as follows:
![\[ \begin{array}{ll} F^a_{i + \frac{1}{2},j} = & E^+_{r; ~ i + \frac{1}{2},j} \Big[ n_{i,j} + \psi(P_{i,j})(n_{i+1,j} - n_{i,j}) \Big] \\ & E^-_{r; ~ i + \frac{1}{2},j} \Big[ n_{i + 1,j} + \psi(\frac{1}{P_{i+1,j}})(n_{i,j} - n_{i+1,j}) \Big] \end{array} \]](form_110.png)
![\[ \begin{array}{ll} F^a_{i,j + \frac{1}{2}} = & E^+_{z; ~ i,j + \frac{1}{2}} \Big[ n_{i,j} + \psi(Q_{i,j})(n_{i,j+1} - n_{i,j}) \Big] \\ & E^-_{z; ~ i,j + \frac{1}{2}} \Big[ n_{i,j + 1} + \psi(\frac{1}{Q_{i,j+1}})(n_{i,j} - n_{i,j+1}) \Big], \end{array} \]](form_111.png)
where 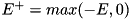 and
and  are used to distinguish the upwind directions for the components of the electric field,
are used to distinguish the upwind directions for the components of the electric field, 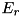 and
and 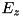 , and we have
, and we have
![\[ \begin{array}{lll} P_{i,j} & = & \frac{n_{i,j} - n_{i-1,j}}{n_{i+1,j} - n_{i,j}}\\ Q_{i,j} & = & \frac{n_{i,j} - n_{i,j-1}}{n_{i,j+1} - n_{i,j}}. \end{array} \]](form_116.png)
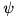 is the Koren limiter function:
is the Koren limiter function:
![\[ \psi(x) = max(0, min(1, \frac{1}{3} + \frac{x}{6}, x)). \]](form_118.png)
The diffusive flux  is calculated using a second-order central differences scheme:
is calculated using a second-order central differences scheme:
![\[ \begin{array}{lll} F^d_{i + \frac{1}{2},j} & = & \frac{D}{\Delta r}(n_{i,j} - n_{i+1,j})\\ F^d_{i,j + \frac{1}{2}} & = & \frac{D}{\Delta z}(n_{i,j} - n_{i,j+1}) \end{array} \]](form_119.png)
and the reaction term  is computed as
is computed as
![\[ S_{i,j} = \sum_{A~\in~{reactions}} \Big[ k_A(|\mathbf{E}|_{i,j}) \prod_{s~\in~{Spec(A)}} n_{s; i,j} \Big] \]](form_121.png)
where 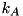 denotes the field-dependent reaction rate coefficient of reaction
denotes the field-dependent reaction rate coefficient of reaction 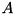 , and
, and 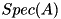 the set of species that appear as an input for reaction
the set of species that appear as an input for reaction 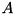 .
.
We compute the net charge 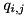 in a cell center by adding up the contributions from the individual charged species:
in a cell center by adding up the contributions from the individual charged species:
![\[ q_{i,j} = \sum_{s~\in~{species}} n_{s; i,j} q_s. \]](form_126.png)
With this net charge, the electric potential 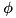 can be computed in the cell centers through a second-order central approximation of the dimensionless Poisson equation:
can be computed in the cell centers through a second-order central approximation of the dimensionless Poisson equation:
![\[ q_{i,j} = \frac{\phi_{i+1,j} - 2 \phi_{i,j} + \phi_{i-1,j}}{\Delta r^2} + \frac{\phi_{i+1,j} - \phi_{i-1,j}}{2r_{i,j} \Delta r} + \frac{\phi_{i,j+1} - 2 \phi_{i,j} + \phi_{i,j-1}}{\Delta z^2}. \]](form_127.png)
From the potential we can compute the components of the electric field from 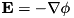 in the cell boundaries:
in the cell boundaries:
![\[ \begin{array}{lll} E_{r; ~ i + \frac{1}{2},j} & = & \frac{\phi_{i,j} - \phi_{i+1,j}}{\Delta r}\\ E_{z; ~ i,j + \frac{1}{2}} & = & \frac{\phi_{i,j} - \phi_{i,j+1}}{\Delta r}. \end{array} \]](form_129.png)
The electric field strength is determined at the cell center, so we have to compute the field components in the center by averaging the values on the boundaries after which we can compute the field strength:
![\[ |\mathbf{E}|_{i,j} = \sqrt{\left(\frac{E_{r;i - \frac{1}{2},j} + E_{r;i + \frac{1}{2},j}}{2}\right)^2 + \left(\frac{E_{z;i,j - \frac{1}{2}} + E_{z;i,j + \frac{1}{2}}}{2}\right)^2}. \]](form_130.png)
The code uses the explicit trapezoidal rule, a second order Runge-Kutta method, for the temporal discretization with time step  . Given some time step
. Given some time step 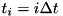 , density distributions
, density distributions  and electric field
and electric field 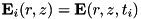 , the densities and field at the next time step,
, the densities and field at the next time step, 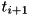 are calculated by first computing an intermediate result for the densities:
are calculated by first computing an intermediate result for the densities:
![\[ \overline{\mathbf{n}}_{i+1} = \mathbf{n}_i + \Delta t F(\mathbf{n}_i, \mathbf{E}_i). \]](form_136.png)
Using these intermediate densities, the potential can be computed by solving the Poisson equation, after which we obtain the intermediate electric field 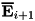 . With this, we compute the final values of the densities at
. With this, we compute the final values of the densities at 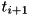 :
:
![\[ \mathbf{n}_{i+1} = \mathbf{n}_i + \frac{\Delta t}{2} F(\mathbf{n}_i, \mathbf{E}_i) + \frac{\Delta t}{2} F(\overline{\mathbf{n}}_{i+1}, \overline{\mathbf{E}}_{i+1}). \]](form_138.png)
Finally, we again compute the potential and electric field, now using the final values of the densities.
The size of the time step  is determined by using a Courant-Friederichs-Levy (CFL) restriction for stability of the advection part of the equations:
is determined by using a Courant-Friederichs-Levy (CFL) restriction for stability of the advection part of the equations:
![\[ \texttt{max} E_r \frac{\Delta t}{\Delta r} + \texttt{max} E_z \frac{\Delta_t}{\Delta_z} < \nu_a. \]](form_139.png)
There are additional restrictions from other diffusion and reaction parts of the equations, but they are dominated by the CFL criterior for the advection part, see Montijn et al.. The value of 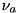 is typically set to 0.25, which is well below the maximum required for stability. We refer the interested reader to the Monograph by Hundsdorfer and Verwer.
is typically set to 0.25, which is well below the maximum required for stability. We refer the interested reader to the Monograph by Hundsdorfer and Verwer.
The ARCoS simulation code contains functions for adaptive grid refinement (also known as adaptive mesh refinement or AMR). Since streamers span different length scales, there is a need to simulate relatively large physical domains while still having high spatial resolution in areas such as the streamer head. To ensure that such large domains can be simulated without giving up resolution and accuracy, the numerical grid is refined adaptively at each time step. The equations are solved on a coarse grid, after which the solution is analyzed using refinement criteria to determine the areas where refinement is needed. The equations are then solved on the refined subgrids after which the process is iterated. Grid generation and grid refinement are performed separately for the density equations and for the Poisson equation.
There are three main refinement criteria. The first two concern refinement of the density grids: Refinement based on the absolute value of 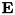 and refinement based on the curvature of densities (both charge density and particle density). The grids used by the FISHPACK solver use their own refinement scheme where the decision to refine is made if the difference between the solution on a grid and the solution on a finer grid exceeds a threshold. The FISHPACK solver is used for both the Poisson equation that determines the electric potential of the system and the Helmholtz equations for the photoionization reactions.
and refinement based on the curvature of densities (both charge density and particle density). The grids used by the FISHPACK solver use their own refinement scheme where the decision to refine is made if the difference between the solution on a grid and the solution on a finer grid exceeds a threshold. The FISHPACK solver is used for both the Poisson equation that determines the electric potential of the system and the Helmholtz equations for the photoionization reactions.
All CDR (Convection-Diffusion-Reaction, CDR is the shorthand term for the density part of the code) refinement criteria are on a per-point basis, which means that the question whether to refine or not is initially answered for every grid cell. This is inconvenient for several reasons, primarily due to the computational cost of such a scheme. The regions containing the streamer head will almost always need to be refined, it is not necessary to evaluate this point-by-point in these regions.
To ease this problem, a minimal refinement area is defined by two parameters:
cdr_brick_dr and cdr_brick_dz, see e.g., file default.cfg . The refinement module divides the grid it receives (this can be the coarsest grid covering the entire domain or a refined grid covering only part of the domain, the code and grid structure are recursive) into "bricks" of these dimensions and searches each brick for cells that match the refinement criteria. Once such a cell is found, the entire brick containing that cell is refined.
For the FISHPACK module, a different approach is used. The refinement routine scans its input grid, starting at the top (  ), going down per "line" (a set of cells with equal
), going down per "line" (a set of cells with equal 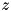 d-coordinate). Once it finds a line with points that meet the refinement criterion it searches for the first line that does not contain any points that meet the criterion. It then refines the smallest rectangular area that contains all the points that meet the criterion. This process is repeated until the bottom (
d-coordinate). Once it finds a line with points that meet the refinement criterion it searches for the first line that does not contain any points that meet the criterion. It then refines the smallest rectangular area that contains all the points that meet the criterion. This process is repeated until the bottom ( 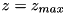 ) of the grid is reached.
) of the grid is reached.

In Figure 2., the black squares represent grid cells at the coarsest level (level 0), the dark gray cells are the first refined sublevel (level 1). Two rectangular grids are included at this level, their shared border is indicated by the red line. The light gray cells show grids at a further refined level (level 2).

The black grid, as shown in Figure 3. is the coarsest level, the dark gray cells are the first refined sublevel, the light gray cells show grids at a further refined level. Each grid has at most one subgrid.
The tree of grids for the density equations may contain refined grids that are adjacent to each other. A schematic showing the nested structure of refined density grids is shown in Figure 2.. The red line in this figure indicates the shared border between two subgrids. For the Poisson-grids, such a structure is not possible and a grid can have at most one refined child-grid as depicted in Figure 3..
The electric field criterion is the most simple of the three refinement criteria. It is an empirical criterion that is not directly motivated by the underlying numerics. A cell with coordinates  qualifies for refinement if:
qualifies for refinement if:
![\[ |\mathbf{E}(r,z)| > E_c \]](form_144.png)
where  is the threshold electric field strength for refinement.
is the threshold electric field strength for refinement.  is a user-determined parameter that is provided in the input file for a run. Since this criterion is independent of the grid level or the cell size, once a cell meets the criterion at the coarsest level, it will also do so at every refined level. Because of this property, the user can limit the refinement depth that is reached through this criterion with the
is a user-determined parameter that is provided in the input file for a run. Since this criterion is independent of the grid level or the cell size, once a cell meets the criterion at the coarsest level, it will also do so at every refined level. Because of this property, the user can limit the refinement depth that is reached through this criterion with the ref_level_eabs input parameter, see e.g., file default.cfg. Setting ref_level_eabs to 1, for example, restricts the refinement from the coarsest level to the first refined level due to the  criterion.
criterion.
The  criterion is inflexible in the sense that it requires the user to have advance knowledge of what the field strengths will be. A possible alternative would be to replace the fixed threshold value
criterion is inflexible in the sense that it requires the user to have advance knowledge of what the field strengths will be. A possible alternative would be to replace the fixed threshold value  by a dimensionless fraction
by a dimensionless fraction 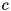 and refine if
and refine if
![\[ |\mathbf{E}(r,z)| > c E_{max} \]](form_148.png)
with 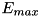 the maximum electric field strength in the computational domain. Since the electric field criterion is mostly empirical, picking the right value for the refinement threshold may be a trial-and-error process.
the maximum electric field strength in the computational domain. Since the electric field criterion is mostly empirical, picking the right value for the refinement threshold may be a trial-and-error process.
There are two criteria that use the curvature of density functions in order to determine which areas to refine. If the curvature is large compared to the cell size, the numerics may become unreliable and it is desirable to work with a finer grid. For a density function 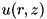 and a cell size
and a cell size 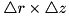 the curvature function
the curvature function 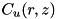 is a discretization of the second derivative of
is a discretization of the second derivative of 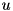 in cylindrical coordinates
in cylindrical coordinates  :
:
![\[ \begin{array}{ll} C_u(r,z) = & \frac{1}{r + \frac{\triangle r}{2}}\Big[(r + \triangle r)\big(u(r + \triangle r, z) - u(r,z)\big) - r\big(u(r,z) - u(r - \triangle r,z)\big)\Big] + \\ & \big[u(r, z + \triangle z) - 2 u(r,z) + u(r, z - \triangle z)\big]. \end{array} \]](form_154.png)
Rather than the absolute value of the curvature, the refinement module looks at the curvature relative to the global maximum, 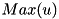 . The final criterion then reads:
. The final criterion then reads:
Refine  if
if 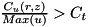
with 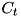 the threshold curvature. This refinement criterion is checked for two density functions
the threshold curvature. This refinement criterion is checked for two density functions 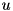 . The first is the (absolute) charge density function. Here an extra condition applies: the absolute value of the charge needs to exceed a certain threshold value (which is hard-coded) before a cell can qualify for refinement based on this criterion. Secondly, the curvature criterion is applied to the particle density functions. Since only mobile particles require a high spatial resolution, any immobile species are not considered in these criteria (which currently excludes all species other than electrons). The computational grids for these immobile species are simply the same as the grids used to solve the density equations for electrons.
. The first is the (absolute) charge density function. Here an extra condition applies: the absolute value of the charge needs to exceed a certain threshold value (which is hard-coded) before a cell can qualify for refinement based on this criterion. Secondly, the curvature criterion is applied to the particle density functions. Since only mobile particles require a high spatial resolution, any immobile species are not considered in these criteria (which currently excludes all species other than electrons). The computational grids for these immobile species are simply the same as the grids used to solve the density equations for electrons.
The FISHPACK module, for the Poisson equation and the photoionization equations, uses a different set of grids than the CDR module and with it a different refinement scheme. Initially, two grids are set up, one coarse and one fine grid (with the fine grid having twice the spatial resolution in each dimension, so 4 times the number of cells). The Poisson/Helmholtz equation is then solved on both grids and the solution of the coarse grid is interpolated onto the fine grid. A grid cell then qualifies for refinement if the absolute difference between the interpolated coarse solution and the fine solution (this difference is called the error) is more than some user-defined threshold. When refinement is needed, a new set of grids is determined using the strategy mentioned earlier and the process is repeated until either the desired accuracy is reached or the maximum number of allowed refinement levels is reached. Since the FISHPACK module was originally only used to solve the Poisson equation for the electrostatic problem and the value of the electric field is defined on the edge of a cell, a cell that does not meet the error-criterion still qualifies for refinement if its neighbor does meet the error-criterion.
One limitation to this scheme is the limited number of grid cells that the FISHPACK routine can handle. Since FISHPACK applies a cyclic reduction scheme, the round-off error increases with the number of grid cells. This places a limit on the size of grids that FISHPACK can solve. Once the refinement module wants to create a grid that is larger than the so-called FISHPACK limit, the refinement attempt is rejected and the code relaxes the error threshold by a factor of 2 and again determines the area to refine, using the new threshold.
To solve the photoionization problem, two Helmholtz equations need to be solved (For details on the implementation of photoionization, the reader is referred to PhD Thesis Wormeester(to appear in 2013), Chapter 3, section Photoionization and references therein). Each of the so-called "photo-terms" has its own characteristic absorption length, which depends on the gas density and oxygen ratio. The term with the short absorption length is often dominated by impact ionization in the head of the streamer, while the term with the long absorption length is the main contributor of electrons in front of the streamer head that are required for a positive streamer to propagate.
The default behavior of the ARCoS code is to treat these two photoionization terms in the same manner as the Poisson problem when it comes to refinement: all user-definable parameters were equal. Since the term with the short absorption length gives rise to a solution that benefits strongly from high spatial resolution (due to the steep gradients) it will easily trigger the refinement criterion. However, it is this term that is dominated by impact ionization, see Luque et al., which reduces the relevance of accurate computation of this term. The user can therefore specify the refinement criteria for each of the two photoionization terms separately, providing the user with the means to allow the important, long absorption length term to benefit from high spatial resolution, while reducing the computational cost incurred by the less important term. However, in tests it was found that tuning the refinement criteria for the photoionization terms has very little effect on computational cost or results.
The adaptive refinement scheme of ARCoS allows for the simulation of large domains while maintaining high spatial resolution in regions that require this. A number of refinement parameters influence both the computational performance and the accuracy of the results, which means that the user has to monitor the results carefully. Since the refinement criteria were setup by Montijn et al.. and Luque et al.. for simulations of air and pure nitrogen, application of the code to other gases may require changes to the values of the various thresholds used in the refinement criteria. An example is high-purity oxygen, with a small nitrogen admixture. In such a gas, ionizing photons will have a very short characteristic absorption length and the calculation of the photoionization terms should be done with high accuracy close to the photon source, primarily the streamer head. However, the limitation of the FISHPACK refinement method does not permit several smaller, adjacent refined sub-grids, which makes it difficult to properly focus on the streamer head without including too much of the channel.
The ARCoS simulation software was originally developed by Alejendro Luque as a more flexible version of the adaptive refinement code developed by Carolynne Montijn as described in PhD Thesis Montijn. The original code by Montijn has been written in Fortran90, while ARCoS has been written in C. The original FISHPACK package used for solving the Poisson and Helmholtz equations is written in Fortran77 and was developed by Adams, Swarztrauber and Sweet. The ARCoS code is now compiled with FISH90, a modernization of the original FISHPACK, employing Fortran90 to slightly simplify and standardize the interface to some of the routines.
ARCoS solves the fluid equations for streamers, described in section Fluid model, on nested Cartesian grids using an adaptive mesh refinement technique. ARCoS allows for the simulation of both positive and negative streamers in the electrode configurations plate-plate and needle-plate. The needle-plate electrode geometry is included using a charge simulation method Luque et al.. This method replaces the electrode needle by a single point charge, with the location and the size of the charge being updated at every time step to ensure the potential at needle tip remains fixed at the predetermined value. The limitation of this method is that the potential on the rest of the surface of the simulated needle will not be accurate. Consequently, the continuity equation is only solved on a smaller grid, not containing the simulated needle.
The effect of this is that ARCoS is not well suited for the study of the inception of streamers, as the area around the tip of the needle is not accurately modelled. However, since inception is often affected by the behavior of individual particles, the use of a particle code such as described in Teunissen et al. and Li et al.. is recommended for studying streamer inception. The purpose of the ARCoS code is to study streamer propagation in the phase after the streamer has formed. Studies performed by Luque et al. show that the dynamics of streamers in later stages hardly depends on initial conditions.
ARCoS allows the user full control over the numerical parameters of the simulation: grid size, refinement criteria and CFL numbers can be set by the user. The kinetic model, i.e., the list of particle species, their reactions and initial densities as well as the diffusion and mobility coefficients can be specified via a series of input files, allowing the user to fine-tune the properties of the gas in which the streamer is simulated, see configuration file input/kinetic_example.cfg.
The ARCoS code can be downloaded from the website http://md-wiki.project.cwi.nl/
Two input parameter files governs all details of the simulation:
libconfig, a free library for processing structured configuration files, is used for reading, manipulating and writing these files. The first file, stored as input/default.cfg, must contain the default values for the global variables. This file is a part of the streamer package distribution. The second file, say input/user_init.cfg, an example is given by input/example_user_init.cfg, has a structure analogously to input/default.cfg, and should contain the parameters which differ from the default values. The program delivers a configuration file, say input/example_user_continue.cfg with the updated parameters from input/user_init.cfg completed with the default values of input/default.cfg.
Since the execution time of a single run will take on the order of several days, it is recommended to split the time period into smaller pieces, and restart the execution several times from the point where the previous run stopped. The easiest way to restart the simulation is
t_end value, the restart value and the name of the load_file. See the end of of this section.The use of the configuration files construction has the following advantages:
It is easy to resume a simulation by using a set of output data as initial conditions. One has to adapt the parameter file with modified start and end times for the simulation. To start a ARCoS simulation use the following command from the directory containing the executables:
The ARCoS program starts and it will print out the parameter values used:
out.example The program will print some extra information to file out.example, e.g., the step size and when a new set of output data has been written, and to which set of file names. Warnings and errors will be printed in file err.example. The program can terminate in three different ways:
In case the simulation runs on a PC or desktop machine, a convenient approach is to set a very large value for the end time and, rather than having the program determine when to terminate, keeping track of the progress of the streamer by checking the output files and manually terminating the program when the desired output is reached, e.g., the streamer has reached the electrode, or, it has started to branch. In other cases, it may be necessary for the program to be able to run for a fixed amount of time. For example when it needs to exit gracefully, which is required for profiling software to work. Also in case of batch jobbing with a limited CPU wall clock time, like on most supercomputers, the end time must be chosen corresponding to the wall clock time.
Data files with periodical data controlled by $output_dt, stored in directory $output_dir, have names using the format variable.C123abc.tsv:
| <variable> | is a particle species or electric field, e.g. charge, d_dummyminus, d_electrons |
| <123> | is the sequence number of that particular output dataset and |
| <abc> | specified the subgrid the output belongs to. |
These files can be used to plot the solution or to restart the simulation. More details on this in the section on output files. To resume the example simulation from output set 123, call:
File and directory handling:
kin_input - The filename of the libconfig input file containing the species, seeds and reactions. By convention, these files have the extension .cfg. output_dir - The directory where the output files will be stored. This can be a relative path to the directory with the executable or an absolute path. When the execution starts, the directory $output_dir must be present and writable. output_dt - The interval (in dimensionless units) with which an output dataset is to be saved. Lower values mean more frequent output, which gives finer grained time-dependent data at the cost of more disk space.Physical parameters:
L_r - Radius of the physical domain in dimensionless units. L_z - Length of the physical domain. Does not include the needle. has_photoionization - Whether to enable the photoionization module.has_photoionization = 1, photoionization is present,has_photoionization = 0, execution without photoionization.photoionization_file - Filename of the file containing the photoionization parameters.E0_z, E0_y, E0_x - Components of the external electric field in dimensionless units. Since the electrodes are located at the top and bottom of the domain 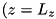 and
and 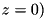 , only
, only E0_z should be nonzero. Positive values of E0_z will generate an electric field in the 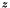 direction, with the top electrode (at
direction, with the top electrode (at 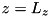 ) having a negative charge, generating negative streamers and vice verse.
) having a negative charge, generating negative streamers and vice verse. pois_inhom - Whether to use a needle-plane geometry or not.pois_inhom = 1 then we have needle-plane case, pois_inhom = 0 gives the plane-plane case. needle_length and needle_radius - The length and radius of the needle in dimensionless units. Only applies when pois_inhom = 1. end_t - Time at which the simulation will stop, in dimensionless units. max_ntheta - Number of azimuthal grid cells. Default max_ntheta = 1. max_ntheta > 1 will activate the full 3D simulation (without cylindrical symmetry) using a pseudo-spectral method described in more detail in Luque et al.(2011).Numerical parameters:
gridpoints_r, gridpoints_z - Number of gridpoints in 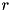 and
and 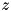 direction for the density equations at the coarsest level.
direction for the density equations at the coarsest level. cdr_max_level - Maximum number of refinement levels of the grid for the fluid equations. cdr_max_level = 0 means no refinement. cdr_bnd_bottom, cdr_bnd_top, cdr_bnd_right - Boundary condition for the density equations at the bottom 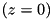 , top
, top  and right
and right 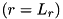 of the domain.
of the domain. cdr_bnd_xxx = 1 gives homogeneous Neumann boundary conditions, cdr_bnd_xxx = -1 gives homogeneous Dirichlet boundary conditions. pois_max_level - Maximum number of refinement levels of the grid for the Poisson equation. pois_max_level = 0 means no refinement. pois_bnd_bottom, pois_bnd_top, pois_bnd_right - Boundary condition for the Poisson equation at the bottom 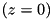 , top
, top  and right
and right 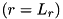 of the domain.
of the domain. pois_bnd_xxx = 1 gives homogeneous Neumann boundary conditions, pois_bnd_xxx = -1 gives homogeneous Dirichlet.In the parameter file input/default.cfg variables and their values are assigned with the following syntax
{
type = "type"; /* type can be a "string", a "double", an "int" */
name = "name"; /* variable name as defined in file include/parameters.h */
comment = "comment"; /* description of the variable, maximum of 100 characters */
value = "value"; /* value of type string, double or integer, related to "type" */
},
# <-- this starts a comment-line, which is ignored.
# White lines are also ignored.
# String-values should be between quotes, numeric values should not
pi=3.14
# (Note: The above is an approximation)
# Scientific notation can be used:
pi_times_thousand=3.14E3
Non-existent or misspelled parameters are ignored. Parameters are not required, every parameter has a default value, which can be found in function init_parameters of src/cstream.c.
The following overview lists the parameters generally meant for testing purposes and changing them is not required for streamer simulations. Therefore they are best left at their default value.
File and directory handling:
cdr_output_margin - Number of margin-cells to be added to the output of the density grids. 2 layers of ghost cells are added on the edge of the computational domain for the purpose of enforcing boundary conditions. With this parameter, these can be included in the output. Value must be smaller than or equal to 2. Default cdr_output_margin = 0. pois_output - Output the grids used in solving the Poisson equation? The grids used for the Poisson equation are different than those used for the density equations as detailed in section Overview of refinement strategies and criteria. pois_output = 0. Note that the absolute electric field is already saved as a density grid, so it is not required to set this parameter to 1 to obtain this data. pois_output_margin - Number of margin-cells to be added to the output of the Poisson grids. Default pois_output_margin = 0. Note : pois_output_margin <= 2.Physical parameters:
start_t - Initial time. This parameter is used when resuming simulations and is automatically updated in that case.Numerical parameters:
The adaptive mesh refinement criteria and the parameters related to them are discussed in more detail in section Overview of refinement strategies and criteria.
ref_threshold_eabs - Refine grid if  exceeds this value.
exceeds this value. ref_level_eabs - Maximum number of refinement levels of the grid for the fluid equation due to the  criterion.
criterion. ref_threshold_charge - Refinement threshold for the curvature of the charge density. ref_threshold_dens - Refinement threshold for the curvature of the particle densities. cdr_brick_r, cdr_brick_z - Size 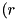 and
and 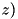 of the minimal refinement area. See Section Size of the refined areas of the density grids.
of the minimal refinement area. See Section Size of the refined areas of the density grids. pois_max_error - An area of the Poisson grid is further refined if the relative error between two consecutive refined levels exceeds this value. nu_a - Courant number based on advection to determine the time step. Note, that nu_a < 1 to satisfy CFL stability. In streamer simulations, this time step restriction will dominate over other parameters (nu_d (diffusion) and nu_rt (reaction)). More details on the time stepping can be found in Time stepping.As mentioned in section Overview , the needle-plane electrode geometry is implemented using a charge simulation technique, which means that the entire needle is represented by a single point charge located on the axis. The position and strength of this charge is updated each time step to ensure that the potential at the point that would be the tip of the needle remains fixed. A schematic depiction of this setup can be seen in Figure 1.. This provides a reasonable approximation of the potential in the area below the needle (the needle is always located at the top of the domain), but the potential will be wrong in the areas to the sides of the needle. Consequently, the density equations are only solved from the tip of the needle and downwards. This means that the computational domain for the density equations is smaller than that for the Poisson equation.
In the specification of the external electric field, E0_z is interpreted as the electric field between the two planar electrodes, far away from the needle. The applied potential is computed as follows:
![\[ V = E_{0,z} * (L_z + L_{needle}) \]](form_166.png)
The code generates a large amount of output files at every output_dt units of simulated time. These output files combined are sufficient to resume the simulation from that time step and can also be used for data analysis. Output files are named variable.C123abc.tsv, where 'tsv' stands for 'Tab-Separated Values'. variable is a particle species or electric field. Examples include electrons, n2plus and eabs (the latter being  ).
). 123 is the sequence number or output time step (which is unrelated to the time step of the numerical scheme) of that output set, it starts at 000 for the first set. This is the initial condition of the system before the simulation starts at 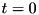 . The alphabetic part of the filename after the output time step,
. The alphabetic part of the filename after the output time step, abc denotes the subgrid contained in that file and this extension is defined recursively. The coarsest grid covering the entire domain has no such alphabetical extension (example: electrons.C123.tsv). At every next level, the subgrids at that level are named a, b, c, ... and this letter is appended to the alphabetical extension. The file electrons.C123ba.tsv contains electron densities at the 123-th time step (so at 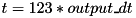 ) for the first subgrid of the second subgrid of the main grid. Beware that since the grid refinement is adaptive, each time step has different subgrids.
) for the first subgrid of the second subgrid of the main grid. Beware that since the grid refinement is adaptive, each time step has different subgrids.

Data, as shown in Figure 4., is stored as plain text, with each line containing a single number. Data is ordered in columns (with fixed  coordinate). So to read the data, use the following pseudo-code:
coordinate). So to read the data, use the following pseudo-code:
for (i = 0, i < rmax*zmax; i++)
{
r = floor(i / zmax);
z = i % zmax;
data[r,z] = read_line_from_file();
}
The dimensions of the grid are not contained in the data files. Instead, for each subgrid and output-step, two additional files are created:
corresponding to subgrid abc of output step 123. The structure of these files is identical to that of the regular data files, but instead of particle densities or electric field strengths, these files contain the  and
and 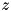 coordinates of the center of the cell corresponding to that line-number. So to determine the coordinates of the
coordinates of the center of the cell corresponding to that line-number. So to determine the coordinates of the 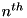 line in a regular data file, simply read the
line in a regular data file, simply read the 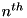 line of the corresponding r and z files.
line of the corresponding r and z files.

The distribution of the ARCoS package contains several directories:
FISH90 - the directory where FISH90 or FISHPACK should be downloadedoutput - this directory may be empty. Its name must correspond to the value of output_dir in file input/default.cfg. Or, the value in input/user_init.cfg if present. python - contains plot files. By means of plotvar pictures can be made of the output files. Not yet implemented. doc - directory with files for Doxygen to generate documentation from source code and this MANUAL. The source of this manual (in MANUAL.md) can be found in its directory markdown. See also the doxygen_config_file. arcos_f90 - a part of the functions in file cdr.c have been replaced by a piece of FORTRAN90 code in order to accelerate the simulation. src - this directory contains the source files written in c. include - this directory contains the include files input - this directory contains all input files. Most of them are libconfig configuration files.The ARCoS simulation software was mostly written in C and its source code is split up in several files, each dealing with a separate part of the program. Most source files have an associated header file (the source file example.c has header file example.h ) containing the type-definitions and preprocessor macros. The function prototypes are aggregated in the header file proto.h. Below is a short summary of the important source files and the functionality that is contained within them.
 1.8.2
1.8.2